阶段综合测试二
第1章~第3章
本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷40分,第Ⅱ卷80分, 共120分,考试时间100分钟.
第Ⅰ卷
1、选择题
1.下列方程是一元一次方程的是
A.2x+5=
B.3x-2y=6
C.
=5-x D.x2+2x=0
2.地球与月球的距离约为384000千米,384000用科学记数法表示为
A.3.84×104 B.3.84×105
C.3.84×106 D.38.4×104
3.下列运算中,结果正确的是
A.
B.
C.
D.
4.把方程
=1-
去分母后,正确的结果是
A.2=1-
B.2x-1=1-
C.2=8-3-x
D.2=8-
5.国庆期间,某楼盘让利于民,将原价为a元/米2的产品房价降价10%销售,降价后的销价格为
A.元 B.10%a元
C.a元 D.a元
6.小明做如此一道题“计算:|+■|”,其中“■”是被墨水污染看不清的一个数,他通过翻看后面的答案,得知该题计算的结果等于6,那样“■”表示的数是
A.3 B.-3
C.9 D.-3或9
7.有理数a在数轴上的对应点的地方如图J2-1所示,则a,b,-a,|b|的大小关系正确的是
图J2-1
A.|b|>a>-a>b B.|b|>b>a>-a
C.a>|b|>b>-a D.a>|b|>-a>b
8.若代数式4x-5与
的值相等,则x的值为
A.1 B.
C.
D.2
9.若方程组
的解x与y的和为0,则m的值为
A.-2 B.0 C.2 D.4
10.如图J2-2是某月的月历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,圈出的三个数的和不可能是
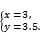
图J2-2
A.69 B.54
C.27 D.40
请将选择题答案填入下表:
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总分 |
答案 |
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷
2、填空题
11.已知方程4x+5y=8,用含x的代数式表示y:__________.
12.已知a3-a-1=0,则a3-a+2018=__________.
13.方程组
的解是
则a+b=__________.
14.若m
15.用m根火柴可以拼成如图J2-3①所示的x个正方形,还可以拼成如图②所示的2y个正方形,那样用含x的代数式表示y,得y=__________.
①②
图J2-3
16.《九章算术》是国内古时候编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图便捷,大家把它改为横排,如图J2-4①②.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图①所示的算筹图用大家目前所熟知的方程组形式表述出来,就是
类似地,图②所示的算筹图大家可以用方程组表述为__________.
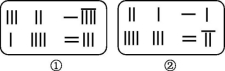
图J2-4
3、解答卷
17.计算:
.
18.先化简,再求值:-
,其中a=1.
19.解方程:
=2-
;
20.下列各数:3.5,-3.5,0.2,-2,-1.6,-
,0.5,其中整数的个数为m,正数的个数为n.
求m2-n2的值;
以上7个数中,绝对值最大的数为__________,绝对值最小的数为__________,有__________对互为相反数的数.
21.已知关于x,y的方程组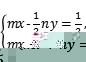的解为
求m,n的值.
22.为了饮水安全,李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水,李明家从甲、乙两个供水点分别购买了10桶和6桶,共花费51元;陈刚家从甲、乙两个供水点分别购买了8桶和12桶,共花费66元.若只考虑价格原因,通过计算说明到哪家供水点购买这种桶装矿泉水更实惠一些?
23.“中国竹乡”安吉县有着丰富的毛竹资源.某企业已回收毛竹52.5吨,依据市场信息,将毛竹直接销售,每吨可获利100元;假如对毛竹进行粗加工,天天可加工8吨,每吨可获利1000元;假如对毛竹进行精加工,天天可加工0.5吨,每吨可获利5000元.因为受条件限制,在同一天中只能使用一种方法加工,并且需要在一个月内将这批毛竹全部销售,为此研究了两种策略:
策略一:将毛竹全部粗加工后销售,则可获利__________元.
策略二:30天时间都进行精加工,将来得及加工的毛竹,在市场上直接销售,则可获利__________元.
是不是存在第三种策略,将部分毛竹精加工,其余毛竹粗加工,并且恰好在30天内完成?若存在,求销售后所获收益;若没有,请说明理由.
阶段综合测试二
1.C2.B3.D4.D5.C
6.D7.A8.B9.C10.D
11.y=
12.201913.314.1或4915.
16.
17.解:原式=4-3-8×
×5=4-3+5=6.
18.解:原式=a2-
a-2-a+1=a2-a-1,
当a=1时,原式=1-1-1=-1.
19.解:去分母,得3=12-.
去括号,得3a-3=12-a-1.
移项、合并相同种类项,得4a=14.
系数化为1,得a=
.
原方程组整理,得
由①,得3y=2x-1③,
把③代入②,得4x-=-5,解得x=-3.
把x=-3代入③,得3y=2×-1,解得y=-.
故原方程组的解为
20.解:在所给的数中,有1个整数,即m=1;有3个正数,即n=3.
当m=1,n=3时,m2-n2=12-32=-8.
3.5,-3.50.2,-
两
21.解:将
代入方程组,得
②-①,得n=,即n=1.
将n=1代入②,得m=1,
故m=1,n=1.
22.解:设这种矿泉水在甲、乙两个供水点每桶的价格分别为x元、y元.
依据题意,得
解得
因为3.5>3,
所以到甲供水点购买更实惠一些.
答:到甲供水点购买这种桶装矿泉水更实惠一些.
23.解:将毛竹全部粗加工后销售,则可获利1000×52.5=52500.
30天时间都进行精加工,将来得及加工的毛竹,在市场上直接销售,则可获利
0.5×30×5000+×100=78750.
存在.设粗加工x天,则精加工天.
依据题意,得8x+0.5=52.5.
解得x=5.
30-x=25.
则销售后所获收益为0.5×25×5000+8×5×1000=102500.
